Longest Palindromic Substring — Solution

dp_table_initial_true_cells

How to Approach the Problem?

My Initial Idea

1. Create a function to check whether a string is a palindrome by comparing characters from both ends.
2. Loop through the string, extract substrings one character at a time, and verify them using the palindrome checker.
3. Store valid palindromes in a list.
4. Return the longest palindrome from the list.

Problems I Encountered

1. I forgot to consider single-character strings as palindromes.
2. My solution failed on inputs like "bb" because I didn’t distinguish between even- and odd-length palindromes.
3. The time complexity was too high (O(n³)) since I was checking all possible substrings.

Final Solution: Dynamic Programming

dp_expansion_steps_with_code

To optimize, I switched to a Dynamic Programming (DP) approach.

Step-by-Step Plan

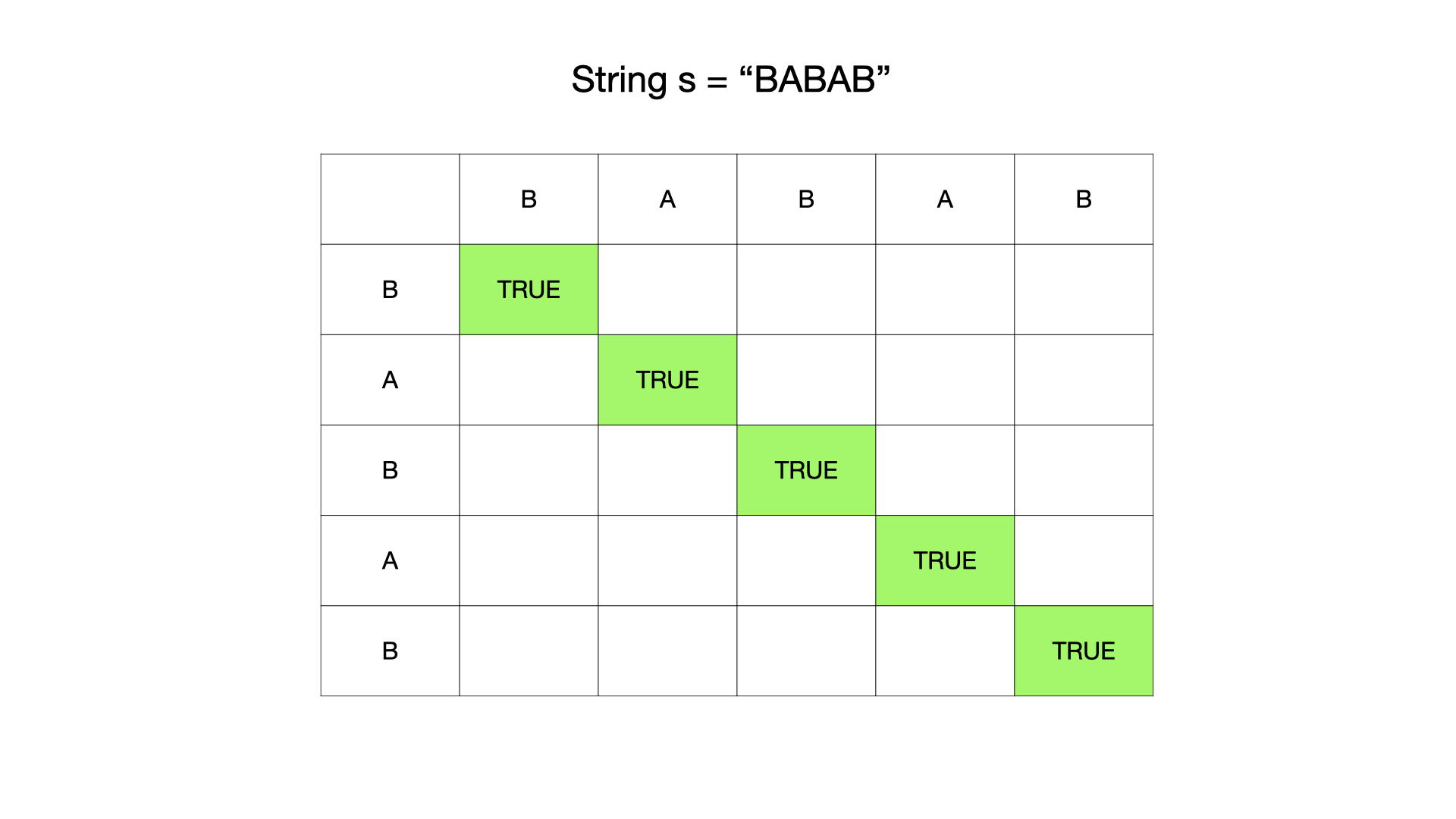
• DP Table Definition:
  dp[i][j] is true if the substring s[i..j] is a palindrome.

• Base Cases:

  • Every single character is a palindrome: dp[i][i] = true
  • Two identical characters are also palindromes:
    dp[i][i+1] = (s[i] == s[i+1])

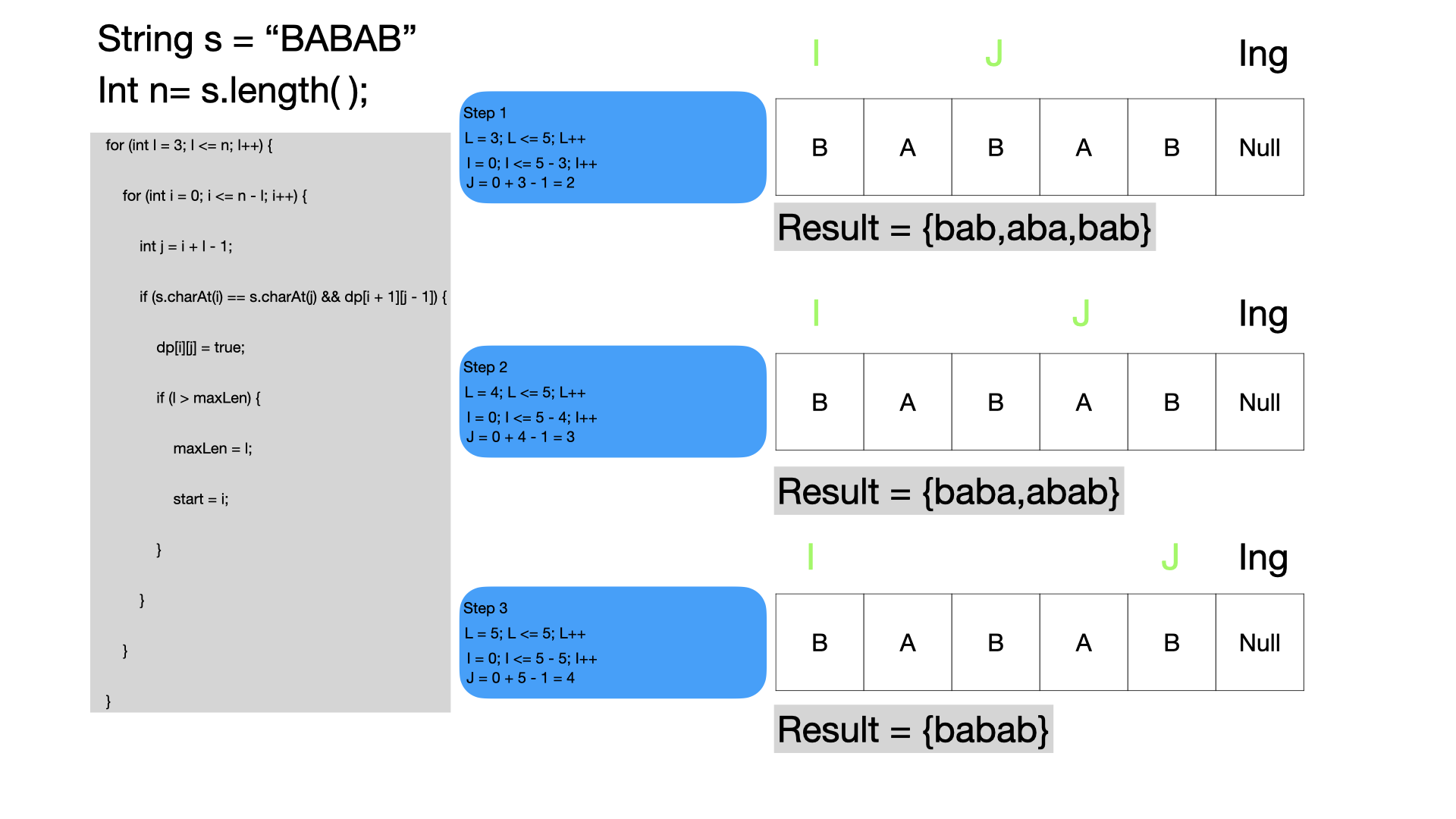
• Transition (Recurrence) Formula:

• dp[i][j] = (s[i] == s[j]) && dp[i+1][j-1];

   for (int l = 3; l <= n; l++) {
       for (int i = 0; i <= n - l; i++) {
           int j = i + l - 1;
           if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {
               dp[i][j] = true;
               if (l > maxLen) {
                   maxLen = l;
                   start = i;
               }
           }
       }
   }
  

final_dp_table_with_true_false

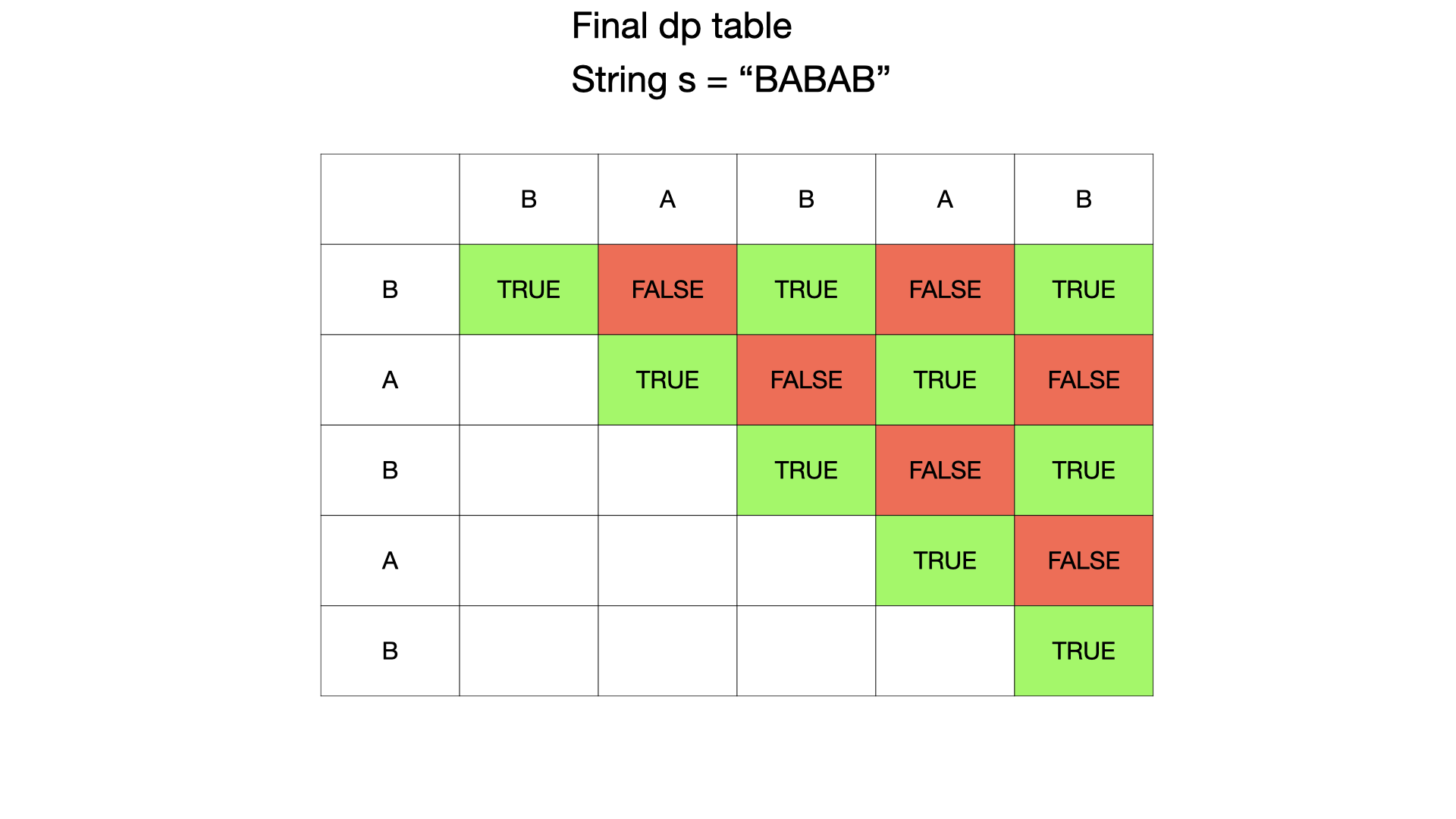
Return the Result
After filling the DP table, return the longest palindromic substring:

return s.substring(start, start + maxLen);

I think I need to keep practicing recurrence relations. I used to understand and solve them easily, but now that I'm trying again after a long time, it feels like I have to start from scratch. I really need to solve algorithms consistently.